La multiplicación es una suma abreviada. Por ejemplo, si necesitamos escribir 8 + 8 + 8 + 8 + 8 + 8, esto es, sumar 6 ochos, para no escribir tanto, el mundo se puso de acuerdo y mejor lo escribimos como 6 x 8. De la misma manera 7 x 5 quiere decir sumar 7 cincos (o también sumar 5 sietes. ¿Podrías decir por qué es lo mismo sumar 5 sietes que sumar 7 cincos?). También como resultado de esto nos tuvimos que aprender las tablas de multiplicar para hacer operaciones rápidamente. Las tablas de multiplicar de la aritmética siguen siendo válidas aquí.
Los números que se multiplican se llaman factores y el resultado se llama el producto o multiplicación
La multiplicación con números reales tiene una dificultad adicional. Como tenemos que multiplicar tanto números positivos como negativos, nos tenemos que aprender la tablita siguiente:
- Producto de números con igual signo nos da un número positivo
- Producto de números con diferente signo nos da un número negativo
Notas:
Por costumbre y para ahorrar escritura en los números positivos se omite escribir el signo +
El signo de multiplicación (x) al que estamos acostumbrados desde la primaria se puede sustituir por el asterisco (*) o por un punto (•) en medio de las cifras que se multiplican las cuales se llaman factores. Por ejemplo las siguientes expresiones significan lo mismo: 2 x 5; 2 * 5; 2 • 5.
Cuando no conocemos, un número utilizamos una letra para representarlo. Por ejemplo con la letra y o con la letra x. Si deseamos multiplicarlo por un número conocido podemos escribirlo así: 7y lo cual se lee siete veces el número y. En este caso no utilizamos ningún signo de multiplicación entre el 7 y la letra porque no se presta a confusión
Si dos números son desconocidos podemos identificarlos con una letra para cada uno y para multiplicarlos solo los ponemos uno junto al otro. Por ejemplo si un número es x y el otro es y, el símbolo xy indica la multiplicación de x por y. esto mismo también lo podemos escribir como x•y (con un punto en el centro) o (x)(y) los dos con paréntesis.
Ejemplos:
1. -a(2) es lo mismo que -a2 = -2a
2. -x(-y) = +xy = xy
3. (5)(5) = 25
4. (5)(-5) = - 25
5. (-5)(5) = -25
6. (-5)(-5) = 25
7. -5 x 10 = -50;
8. -0.1 x -100 = +10;
9. 7 x 30 = +210;
10. 12 x -1000 = -1200
11. -4 (-8)7=224
12. (-2)(-2)(-2)(-2) = +16
13. (-2)(-2)(-2)(-2)(-2) = -32
14. –(2)(2) = -4
15. –(-2) = 2
16. -22= -(2)(2) = -4
17. (-2)2 = (-2)(-2) = +4
5.2 Propiedad distributiva de la multiplicación con la suma y la división de números Reales
Existe una propiedad que se aplica juntamente a la suma y a la multiplicación. Se llama propiedad distributiva de la multiplicación con respecto a la suma o simplemente propiedad distributiva.
La debemos aplicar cuando se tiene una multiplicación como esta: a • (b + c). Quiere decir que se desea multiplicar un número por la suma de otros dos números. Esta ley la escribimos matemáticamente como sigue:
Sean Si a, b, y c son todos números reales entonces a • (b + c) = ab + ac
Esto quiere decir que si tenemos la multiplicación 5 • (4 + 9), el resultado se puede obtener de dos maneras. La primera sumando el 4 mas el 9 lo cual da 13 y después multiplicando por 5 lo cual produce 65. La segunda manera es aplicar la propiedad distributiva. Multiplicamos primero el 5 por el 4 y le sumamos el resultado de multiplicar 5 por 9; es decir:
5 • (4 + 9) = 5 • 4 + 5 • 9 = 20 + 45 = 65
Cuando lo que está dentro del paréntesis no se puede sumar debemos porque son letras debemos utilizar la propiedad distributiva.
Ejemplo 1:
7(10w +20z); En este caso no podemos sumar lo que está dentro del paréntesis porque son cosas diferentes. La w representa a un número desconocido y la z a otro número que puede ser distinto al representado por la w. Así es que no sabemos cuánto es 10w +20z. En este caso debemos utilizar la propiedad distributiva. Así es que el resultado es:
7(10w +20z) = 70w + 140z
Ejemplo 2:
-2(3 + 6) = -2 • 3 + (-2) • 6 = -6 + (-12) = -18
2y + 3y = y(2 + 3) = y5=5y
5.3 La División de números reales
De la misma manera que para definir la resta recurrimos a algo que ya sabíamos, como era la suma, para definir la división de números reales recurrimos a cosas ya conocidas, en este caso la multiplicación.
Tenemos el siguiente problema ¿Por cuánto debo multiplicar a un número a para obtener otro número b?. Esto es . Recordemos lo que hicimos para la resta. En este caso solo sabemos multiplicar así que llamamos a la interrogación x, y multiplicamos ambos miembros de esta igualdad por el inverso multiplicativo de a, tenemos:
De aquí tenemos:
y por lo tanto el número desconocido x es:
Pero es mejor utilizar el símbolo b ÷ a , que lo leeremos como b entre a, en lugar de la letra x. Por lo tanto tenemos qué:
Nota: Si sustituimos este número encontrado
en el lugar de la interrogación de la pregunta inicial, podemos comprobar que realmente resuelve el problema inicial que planteamos: “¿Por cuánto debo multiplicar a un número a para obtener otro número b?” porque:
Diremos que dividir un número b (llamado dividendo) entre otro número a (llamado divisor) es multiplicar al número b, por el inverso multiplicativo del número a. En otras palabras, para realizar una división debemos convertirla primero en una multiplicación utilizando el inverso multiplicativo del divisor. Para indicar una división utilizamos el signo entre (÷). Así por ejemplo p ÷ q quiere decir dividir p entre q; -45÷10 significa dividir -45 entre 10.
Lo anterior quiere decir que si tenemos que dividir dos números, debemos convertir la división en una multiplicación del dividendo por el inverso multiplicativo del divisor.
Ejemplo: ;
Más ejemplos




Nota importante: Fíjate que si por ejemplo dividimos 4 ÷ 5 eso se convierte en
por nuestra definición de división. Pero esto quiere decir sumar 4 veces
, esto es:
Esto último da como resultado
lo cual quiere decir finalmente que
o lo que es lo mismo:
Por lo tanto
a la vez que es un número racional o quebrado, también es una manera de representar la división de 4 entre 5. Si generalizamos lo que acabamos de ver para todos los números reales, concluimos que todo quebrado también indica una división del numerador entre el divisor, esto es:
Ojo. El 0 no tiene inverso multiplicativo, en otras palabras, no existe ningún número que multiplicado por el 0 nos de 1 como resultado. Así que será torturado, multado y reprobado cualquier alumno que se atreva a proponer algún número como inverso del 0. Así pues será un gravísimo error decir que el inverso del 0 es
El 0 no tiene inverso y por lo tanto no se puede dividir entre 0
El 0 no tiene inverso y por lo tanto no se puede dividir entre 0








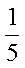







buenisima explicacion mil gracias :)
ResponderEliminarte equibocastes LOLLLLLLLLLLLLLLLLLLLLLLLL
ResponderEliminar*equivocaste.
EliminarDebes pensar antes de escribir.
jejjeje gays
Eliminarquien me puede explicar esto
EliminarMateo El no se equivoco!
EliminarUish! Grocero :3
EliminarUish! Grocero :3
Eliminaryyyyyyyyy no sabe diciiir
EliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
EliminarEso a side lo Mejia
Eliminarjejeej gays
ResponderEliminarMuy buena explicacion MUCHAS GRACIAS :D
ResponderEliminarMuy buena explicación y ejemplos, me sirvió mucho para mi micro clase en el salón. Muchisimas gracias,este material casi no se encuentra.
ResponderEliminarMuy buena explicación y ejemplos, me sirvió mucho para mi micro clase en el salón. Muchisimas gracias,este material casi no se encuentra.
ResponderEliminarMe la chupad
ResponderEliminarMe la chupad
ResponderEliminarno me sirve
ResponderEliminarEsto esta super para el q lo sabe entender
ResponderEliminarClaro K si para quien lo puede engender
ResponderEliminarpendejos comentarios es lo unico q veras aqui
ResponderEliminar